MCMC，即传说中的Markov Chain Mento Carlo方法。其主要用于统计推理中进行模拟抽样，尤其在贝叶斯推理中有着非常广泛的应用。如算法模型的后验参数估计问题，很多情况下其后验概率分布没有确定性的解析解，或者解析解计算起来非常复杂，便可以通过MCMC模拟抽样，根据大数定律，参数的期望便可以通过对抽样样本的求均值来评估。

山人第一次见到MCMC兄还是在研究僧阶段，那时候以Latent Direichlet Allocation(LDA)为代表的Blei先生的一系列主题模型算法还很火，甚至你还能看见Andrew Ng的身影。于是导师欣然的把其另一篇层次主题模型的论文，Hierarchical LDA(hLDA)甩给我们，拍着我们的肩膀，语重心长的说，好好干，会很有前景的。于是我的MCMC初体验是这样的：
What the hell? 于是直到现在还对MCMC念念不忘。好吧，是耿耿于怀。最近又看见Quora上有人讨论MCMC和Gibbs抽样，再看时，发现虽然有一两年未看，脑部神经元还是不停的工作，现在理解起来竟然清晰许多。 MCMC是Markov Chain和Mento Carlo两个概念的组合，我们不妨分而治之，先看看各自的含义。

I-Markov Chain

即马尔科夫链，这哥么大家肯定不会陌生，还记得Hidden Markov Model么（Baum-Welch算法会推导了么:( )马尔科夫链的一个重要属性就是无记忆性。其表示的随机过程，在一个状态空间里游走且未来的状态只与当前的状态有关，而与之前的状态均无关。这种无记忆性便称之为马尔科夫性。
$$ p\left( x^{t+1} | x^{t},x^{t-1}...\; x^{1} \right)\; =\; p\left( x^{t+1} | x^{t} \right)\tag{1} $$ 马尔科夫链是一种随机过程，其定义有主要有两点，即状态空间和转移概率矩阵。如下图所示，一个简单的马尔科夫链随机过程，包含三个状态：

其状态之间的转移概率矩阵如下：
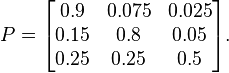
假设在状态\(\Pi_{i}\)时，你在Bull Market 状态，且当前概率分布为\(\left[ 0,\; 1,\; 0 \right]\)。在下一个\(\Pi _{i+1}\)状态时的概率分布为
$$ \Pi _{i+1}\; =\; \Pi _{i}\; .\; P\tag{2} $$ 则结果为\(\Pi _{i+1}\;=\;\left[ .15\; \; .8\; \; .05 \right]\)。如此类推，下一个状态分布则为： $$ \Pi _{i+1}\; =\; \Pi _{i}\; .\; P^{2}\tag{3} $$ 如此下去，最终发现我们会得到一个稳定的状态，此时 $$ \Pi \; =\; \Pi \; .\; P\tag{4} $$ 即状态分布变得稳定(Stationary)，不会再随着状态转移概率的变化而变化。且我们发现，即使我们的初始状态分布矩阵不是\(\left[ 0,\; 1,\; 0 \right]\)而是另外一个值，如\(\left[ 0.4,\; 0.3,\; 0.3 \right]\)时，最终经过多次转移，也会达到最终的稳定(Stationary)状态，且稳定状态的分布是一致的，即最终的Stationary状态与初始分布矩阵没有关系，只与状态转移矩阵有关。那末是不是所有的状态转移矩阵都能最终达到稳定状态呢？答案自然不是，还是需要马氏链定理的保证，简单说就是
如果一个非周期马氏链具有概率转移矩阵\(P \)，且它的任何两个状态都是联通的，那么如果\(l\mbox{im}_{n\; ->\infty }\; P_{ij}^{n}\; =\; \pi \left( j \right)\)存在且仅与j有关，那么这样的一个稳定分布就是存在的。
这里还有一点山人刚开始时也是非常模糊。就是很多算法中提到，当经过了burn-in阶段，状态分布稳定以后开始取样计算概率分布，当时就想，既然都稳定了，\(\pi \)都保持不变了，取的样本不都一样么？其实这里所说的状态稳定是指满足了某一个概率分布，即稳定后抽样出的样本都是同分布的。而在稳定之前则可能不同的样本是产生自不同的概率分布。

II-Monte Carlo

说完了马尔科夫再来说说蒙特卡洛方法吧，其名子来源于摩纳哥的蒙特卡洛赌场，是一种通过模拟抽样求积分的方法。一个经典的应用便是计算圆周率。这个名叫“hit and miss"的实验过程为：假设有一个单位长度为1的正方形区域，再以正方形的中心为圆心，单位长度为半径画一个正方形的内切圆。有一个随机数发射器随机的往正方形区域里发射。当经过N多次以后，圆周率可以估算为(hawaii.edu)： \(\pi \; =\; \frac{4N_{hit}}{N_{shot}}\)

大学微积分中我们学过常见函数求积分的方法，如\(I\; =\; \int_{\theta }^{\infty }{g\left( \theta \right)p\left( \theta \right)d\theta }\)，p是\(\theta \)的概率密度函数，求其在g上的积分。但在实际应用中，函数g往往是不可积的，且\(\theta \)可能是高纬向量，使得我们很难求得其解析解。在大数定律和中心极限定理的保证下，蒙特卡洛方法则通过模拟抽样的方法为求其近似解提供了一条途径。我们可以通过从概率密度函数p中抽样出\(\theta \)，最终MC近似的解为：\(I^{'}\; =\; \sum_{i=1}^{M}{g\left( \theta _{i} \right)}\)。
应用到贝叶斯推理中，如果我们能够通过抽样的方式从参数变量的联合分布中抽取到足够多的样本数据，我们便可以通过贝叶斯参数估计等方法求得其近似值。但往往参数的联合分布各个变量并非独立，且很复杂。尤其如LDA等主题生成模型里，要对联合分布抽样几乎是不可能的。有么有可能通过某种控制变量法，对条件概率进行抽样，借用马尔科夫链中条件概率转移矩阵达到稳定状态后的概率分布就是其变量的联合分布下的样本点呢？

III-MCMC类方法

于是，为了避免构造一个复杂繁琐的联合分布函数来进行蒙特卡洛抽样，MCMC类方法神兵天降。通过构造一个状态转移概率矩阵，那末当其到达稳定状态时，分布便是所求的联合概率分布。而联合分布函数的样本点则是每一次状态转移时自然产生的。这么牛掰的想法当然不是山人想到的，一个叫着Metropolis的哥么在1953年研究粒子系统的平稳性质便提出来了。而目前我们常用的一个叫着Metropolis-Hastings算法便是在其基础上的一个改进。

1 细致平稳条件

我们在前面提到了，我们可以通过构造一个状态转移概率矩阵，使得其平稳状态下的概率分布就是我们想要的分布。但不是随意构造一个状态转移概率矩阵就能满足的。那需要什么样的条件呢？细致平稳条件就是这样一个充分条件。如果非周期马氏链的转移概率矩阵\(P\)和分布\(\pi \left( x \right)\)满足：
$$ \pi \left( i \right)P_{ij}\; =\; \pi \left( j \right)P_{ji}\; for\; all\; i,j\tag{5} $$ 则\(\pi \left( x \right)\)就是该马氏链的平稳分布。那自然不是所有的概率矩阵和分布都满足等式（5）中的条件，我们可以通过对马氏链进行一个小小的改造： $$ \pi \left( i \right)P_{ij}\alpha \left( i,j \right)\; =\; \pi \left( j \right)P_{ji}\alpha \left( j,i \right)\tag{6} $$ 于是新得到的马氏链为\(P '(j,i)\)： $$ \label{detailed-balance} \pi (i) \underbrace{p(i,j)\alpha(i,j)}_{P '(i,j)} = \pi (j) \underbrace{p(j,i)\alpha(j,i)}_{P '(j,i)} \quad (**) \tag{7} $$ 而只要通过对称性，取\(\alpha \left( i,j \right)\)为\(\pi \left( j \right)p\left( j,i \right)\)，取\(\alpha \left( j,i \right)\)为\(\pi \left( i \right)p\left( i,j \right)\)即可。此处的\(\alpha \left(.\right)\)称之为接受率。其可以理解为，在原来的马氏链上，从状态\(i\)以\(p\left( i,j \right)\)的概率跳转到状态\(j\)时，我们以\(\alpha \left(i,j\right)\)的概率接受这个跳转。
一般的MCMC采样算法的接受率通过和一个Uniform[0,1]分布采样的值u作比较，如果接受率大于这个值，则接受这次转移，从i转移到j状态，反之则保持原i状态。但是我们在实际应用中使用这个方法时发现，很多情况下接受率普遍很低，导致马氏链状态转移缓慢，最终收敛的速度非常慢。为了解决这个问题，我们还是采用类似等式（6）的方法，分子分母的接受率同步增大。
$$ \frac{\alpha \left( x,y \right)}{\alpha \left( y,x \right)}\; =\; \frac{\pi \left( y \right)p\left( y,x \right)}{\pi \left( x \right)p\left( x,y \right)} $$ 我们可以把跳转之后的状态\(\alpha \left( y,x \right)\)接受率为1，则我们可以得到下面的接受率公式(注意接受率取值范围只能是[0,1])：
$$ \alpha \left( i,j \right)\; =\; \min \left\{ \frac{\pi \left( j \right)p\left( j,i \right)}{\pi \left( i \right)p\left( i,j \right)},\; 1 \right\}\tag{8} $$tag{8} 按照式（8）的接受率，便是我们的Metropolis-Hastings算法。

2 Gibbs抽样

当变量状态多，且维度比较高时，MH算法的接受率仍然差强人意。要是每次都接受该多好啊。那什么样的情况下，我从\(i\)到\(j\)时，每次都能接受呢？（即接受率为1）。最终发现，我们每次可以沿着垂直于某个变量维度的轴走。即通过迭代的方法，每一次只对一个变量进行采样。举一个二维空间的例子，假设一个概率分布\(p\left( x,y \right)\)，来看\(x\)坐标相同的两个点\(A\left( x_{1},\; y_{1} \right)\)和\(B\left( x_{1},\; y_{2} \right)\)，通过简单的联合概率和条件概率的关系我们可以得到：
$$ p\left( x_{1},\; y_{1} \right)p\left( y_{2}| x_{1} \right)\; =\; p\left( x_{1} \right)p\left( y_{1}| x_{1} \right)p\left( y_{2}| x_{1} \right)\tag{9} $$ $$ p\left( x_{1},\; y_{2} \right)p\left( y_{1}| x_{1} \right)\; =\; p\left( x_{1} \right)p\left( y_{2}| x_{1} \right)p\left( y_{1}| x_{1} \right)\tag{10} $$ 很明显，等式(9),(10)右边是相等的，如(11)所示: $$ p\left( x_{1},\; y_{1} \right)p\left( y_{2}| x_{1} \right)\; =\; p\left( x_{1},y_{2} \right)p\left( y_{1}| x_{1} \right)\tag{11} $$ 下图给出了一个更直观的表示：

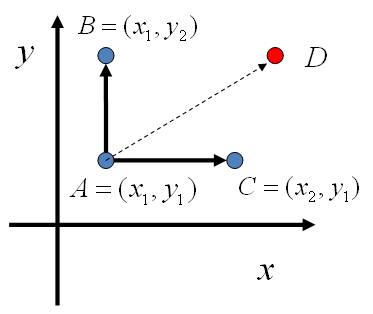
即，从A到B和从B到A的转移是直接满足细致平稳条件的。因此我们不需要等式(6)中的接受率来帮忙，即接受率为1.图中假设初始状态为A，则从A到下一个概率转移矩阵分别为：
$$ Q\left( A\; ->\; B \right)\; =\; p\left( y_{B}| x_{1} \right) $$ $$ Q\left( A\; ->\; C \right)\; =\; p\left( x_{C}| y_{1} \right)
$$ $$ Q\left( A\; ->\; D \right)\; =\; 0\tag{12} $$ 因此类似于曼哈顿距离的方法，状态转移总是沿着横平竖直的街区进行。这边是Gibbs抽样算法的核心思想。下图给出了一个Gibbs抽样的直观图。

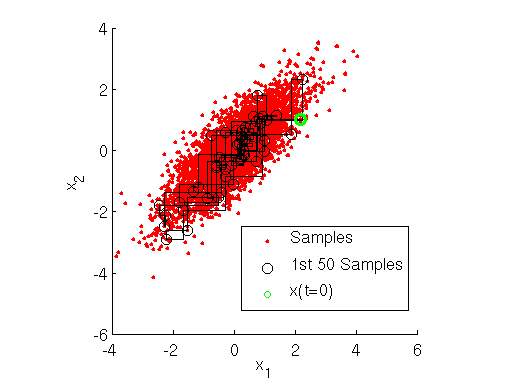
3 收敛条件的判断

我们都知道当概率状态转移稳定时，其分布便是所要求的联合概率分布。但我们不可能通过如等式(2),(3)的方法来每转换一步就求其概率分布，比较是否改变。主要原因有二，其一是不可把所有变量间的转移概率都找到，其二矩阵计算耗时耗力。常见的方法便是通过burn-in的方法，多跑几次。也有通过计算当前状态下的联合分布可能性函数，然后根据Autocorrelation Function(ACF)的变化速率来判断迭代是否收敛。
So long, and thanks for all the fish.

参考

[1] PRML读书会第十一章 Sampling Methods
[2] LDA-math-MCMC 和 Gibbs Sampling
[3] Burn-In is Unnecessary
[4] One Long Run in MCMC
[5] What-are-Markov-Chain-Monte-Carlo-methods-in-laymans-terms
[6] MCMCAlgorithmsBeta_Distribution