理解支持向量机(Support Vector Machine, SVM)的角度很多。从分类问题入手,由最小化训练错误导出限制条件下的凸优化问题的解,进而由线性可分的硬边界泛化为利用松弛变量放宽限制条件的软边界问题;从一般性的损失函数出发,由线性回归的0-1损失函数换成hinge损失函数,进而加上针对模型复杂度的L2惩罚项;亦或是从支持向量的角度,由核函数的一般应用到稀疏核的支持向量,进而分析SVM的核技巧。后者学习曲线相对来说比较大,却有助于深入理解SVM。
(不知是从哪来的先入为主,以前提到SVM,脑中总是出现一些非常confusing的概念,什么最大边际,Lagrange对偶性,最小最大化一系列公式,本来打印好好的论文,没看到优化目标函数呢,就放之一旁等着毕业卖废纸了。山人也觉得没得治了。好吧,从此篇开始就自称山人了: (,但当山人看到下面关于一个SVM的段子时,对它的热情又从新燃起了。)

I- 非线性变换
很多算法在处理输入空间的样本时,会把输入空间的生数据样本转换成特征空间的样本表达。有时这是一种显式的的特征选择,如去噪或提取更高层表达能力的特征。有时这是为了解决样本在生输入空间不可分,而进行的高维空间变换,从而把原本不可分的数据变换成在高纬可分的特征点。而这个映射便是通过非线性变换来实现的。一个直观的例子:
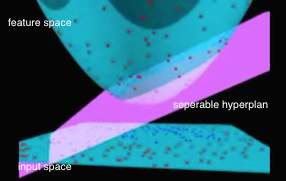
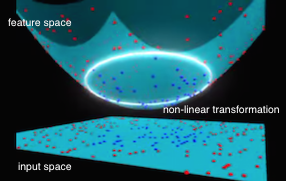
如上图所示,原始的二维平面上是遍布生数据的输入点,其类别标签用红点和蓝点来区分。由左图中平面上点的分布来看,在输入的二维空间是线性不可分的。但我们可以通过一个寻找一个特征映射函数\(\phi \left( . \right)\)来把输入空间的点\(x\),映射为三维特征空间中的点\(\phi \left( x \right)\),于是这个三维空间中的点便可以通过左图中一个粉红色的超平面来分隔。但即使在三维特征空间可分,我们怎么把这个三维特征空间的分隔超平面映射回二维输入空间去呢?很简单,我们可以直接把超平面与特征空间圆锥体的截平面直接投影到二维空间里去,所形成的椭圆曲线就是二维空间的分隔线。如上面右图中的白色所示。
II- 核方法
核方法便是基于非线性特征映射,定义如下:
$$
k\left( x,x' \right)\; =\; \phi \left( x \right)^{T}\phi \left( x' \right)\label{p}\tag{1}
$$
其是在大边际分类器背景下被重新引入机器学习,进而催生出了SVM。而伴随着SVM的显著效果和广泛引用,越来越多的核方法被引入。通过它,便可以把一些原本在低维不可分的数据集映射到高维可分空间。映射到高维空间后的数据点便可以通过高维空间中的简单线性计算来达到可分的目的。但是,这个过程可能需要两步:第一,是找到某种上面所说的非线性变换的映射\(\phi \left( x \right)\), 把所有的低维空间的点变换成高维空间的点。第二,是在高维空间中找到一种简单的线性可分函数来对这些映射后的点进行分类。而其中面临的一个问题就是映射后的空间维度往往非常的高,其向量点积的运算非常的耗时费力。有些情况下,为了实现高纬可分,映射后的维度可能是无限维度。而在这么高纬度的空间进行向量运算变得非常困难。所以说,即使我们能够想象到这样一种高维特征映射的方式,以现代的计算能力来看,成本还是太高了。
核函数恰恰就像连接低维空间和高维空间的虫洞,我们可以通过它,在低位空间直接计算高维空间。正如时空中的虫洞由于星体旋转和引力作用飘忽不定,在算法上使用核函数也是有限制条件的。如上述定义(1)所述,算法必须能表示成两个变量的非线性映射的点积。
核函数也有其重要的属性,如连续,对称,一般情况下需要是半正定的Gram矩阵。而正定核能够保证是凸优化问题,且有唯一解。
实际应用中可选择的内核函数有很多,如线性内核,多项式内核,高斯内核,sigmoid内核等。就如内核函数本身一样,如何根据实际的数据集特征选择合适的内核也是非常tricky的事。我们往往需要根据样本数,特征数,数据可视化后数据特征与类别的关系来综合选择。
1.线性内核
使用线性内核,其实就等价于没有内核,特征映射的过程是简单的线性变换。公式如下所示:
$$
k\left( x,y \right)=x^{T}y\; +\; \mbox{C}\tag{2}
$$
常量C便是非线性内核的可选参数。通常情况下,线性内核的适用场景很多,很多线性可分,甚至线性不可分的数据集,使用线性的效果往往比非线性的要好。尤其是在数据集很大,且特征很多,或是特征远大于数据集时,线性内核便往往能够取得很不错的效果。且其相对于其他非线性内核,训练时要快的多。
2.多项式内核
$$
k\left( x,y \right)=\left( \alpha x^{T}y\; +\; \mbox{C} \right)^{d}\tag{3}
$$
当维度\(d\)过大时往往容易造成过拟合问题。通常2度的多项式内核在用来特征选择的时候非常有用。
3.高斯(RBF)内核
$$
k\left( x,y \right)\; =\; \exp \; \left( -\frac{\left| \left| x-y \right| \right|^{2}}{2\sigma ^{2}} \right)\tag{4}
$$
其另外一种表达:
$$
k\left( x,y \right)\; =\; \exp \left( -\gamma \left| \left| x\; -\; y \right| \right|^{2} \right)\tag{5}
$$
Where \(\gamma\) > 0。高斯内核属于经典的RBF内核,线性内核也属于一种特殊的RBF内核。一般来说,RBF内核是首选,尤其对于那些类别和特征值呈非线性关系的数据集。相对于多项式内核,RBF超参要少,相对更为简单。且\(0 < K_{i,j} < 1\),相对于多项式内核可能从0到无限大之间,其数值计算的压力也会少很多。而sigmoid的Gram矩阵是条件正定的,使用范围受限。RBF内核则没有这个问题。但值得一提的是,RBF内核和L2 Regularization类似,倾向于选择平滑的特征。在本文分类中,线性内核往往训练比起更为高效,且性能相差无几。
4.Sigmoid 内核
$$
k\left( x,y \right)\; =\; \tanh \left( \alpha x^{T}y\; +\; \mbox{C} \right)\tag{6}
$$
Where \(\alpha\)可以视为一个scaling 参数,常数\(C\)则是shifting参数。sigmoid内核起源于神经网络,activation函数使用的也是sigmoid function,而每个节点的数据向量也是线性权重组合。使用sigmoid内核的SVM模型等价于一个两层感知机。虽然其是conditionally positive definite, 实际应用发现也能够有很好的性能。台大的一篇论文讨论过选择sigmoid内核参数的问题。
 关于各个内核的对比,quora上有一篇从parametric和nonparametric角度的问答,相当经典。
关于各个内核的对比,quora上有一篇从parametric和nonparametric角度的问答,相当经典。
III- 从稀疏内核机到SVM
定义(1)中提到的基于非线性映射的内核方法是基于所有\(x\; \cdot \; x'\)训练数据对的。核函数虽然能够将高维空间的非线性映射特征直接在原始空间计算,但当训练样本过多时,这样的计算也是费时费力的。有没有可能做进一步的特征集选择,过滤到无关的样本点。如下图所示:
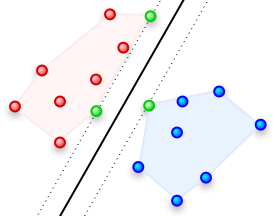
如果我们想正确的划分出红点和蓝点,我们只要保证分割的线在左边的两个绿点和右边的一个绿点之间便可以,而无需去考虑所有其他的红点和蓝点,因为他们对于我们能否正确分类,没有任何决定性作用。那么我们为何苦费时费力的计算所有的数据点呢?答案当然是没有必要。我们在核方法上进行稀疏特征选择便是稀疏内核机。而最大分类边际便是其特征选择方法。
当然哪些特征点能够产生最大分类边际不是我们看到这幅图就能凭空想出来的。据说最初做SVM分类时,选的也是定义(4)所用的高斯内核。他们没有直接使用最小化误分类率的决策平面,而是通过最小化学习到的密度模型的错误概率来确定最优超平面。结果发现,当\(\sigma ^{2}\)极限于0时,达到最大边际。即当\(\sigma ^{2}\)越接近于0,那些边上无关的红点或蓝点对于最终错误率的影响越小。最终当达到极限时,只有这些绿点对其有贡献了。而这些绿点便是所说的支持向量。于是SVM的优化目标就成了在正确分类的情况下,最大化分类边际。这个最大边际则是一种稀疏特征选择。
参考
[1] Kernel Functions for ML Applications.
[2] A Practise Guide to SVM Classification.
[3] Pattern Recognition and Machine Learning.