在线性代数，函数分析等数学分支中，范数（Norm）是一个函数，其赋予某个向量空间（或矩阵）中的每个向量以长度或大小。对于零向量，另其长度为零。直观的说，向量或矩阵的范数越大，则我们可以说这个向量或矩阵也就越大。有时范数有很多更为常见的叫法，如绝对值其实便是一维向量空间中实数或复数的范数，而Euclidean距离也是一种范数。

范数的一般化定义：设\(p\geq 1\)的实数，p-norm定义为：

$$ \begin{align} \left| \left| x \right| \right|_{p}\; :=\; \left( \sum_{i=1}^{n}{\left| x_{i} \right|^{p}} \right)^{\frac{1}{p}}\label{p}\tag{1} \end{align} $$
此处，当\(p=1\)时，我们称之为taxicab Norm，也叫Manhattan Norm。其来源是曼哈顿的出租车司机在四四方方的曼哈顿街道中从一点到另一点所需要走过的距离。也即我们所要讨论的l1范数。其表示某个向量中所有元素绝对值的和。 而当\(p=2\)时，则是我们最为常见的Euclidean norm。也称为Euclidean distance。也即我们要讨论的l2范数。 而当\(p=0\)时，因其不再满足三角不等性，严格的说此时p已不算是范数了，但很多人仍然称之为l0范数。 这三个范数有很多非常有意思的特征，尤其是在机器学习中的正则化（Regularization）以及稀疏编码（Sparse Coding）有非常有趣的应用。
下图给出了一个Lp球的形状随着P的减少的可视化图。lp ball

1- L0 范数

虽然L0严格说不属于范数，我们可以采用等式\(\ref{p}\)来给出l0-norm得定义：

$$ \left| \left| x \right| \right|_{0}\; :=\; ^{0}\sqrt{\sum_{i=0}^{n}{x_{i}^{0}}}\tag{2} $$
上面的公式仍然让人不是很明白，0的指数和平方根严格意义上是受限条件下才成立的。因此在实际应用中，多数人给出下面的替代定义：
$$ \left| \left| x \right| \right|_{0}\; \; =\; \#\left( i \right)\; with\; x_{i}\; \neq \; 0 \tag{3} $$
其表示向量中所有非零元素的个数。正是L0范数的这个属性，使得其非常适合机器学习中稀疏编码，特征选择的应用。通过最小化L0范数，来寻找最少最优的稀疏特征项。但不幸的是，L0范数的最小化问题在实际应用中是NP难问题。因此很多情况下，L0优化问题就会被relaxe为更高维度的范数问题，如L1范数，L2范数最小化问题。

2- L1 范数

对于向量X，其L1范数的定义如下：

$$ \left| \left| x \right| \right|_{1}\; :=\; \sum_{i=1}^{n}{\left| x_{i} \right|} \tag{4} $$
其应用范围非常的广泛。如在计算机视觉中的Sum of Absolute Differents，Mean Absolute Error，都是利用L1范式的定义。
L1最优化问题的解是稀疏性的，其倾向于选择很少的一些非常大的值和很多的insignificant的小值。而L2最优化则更多的非常少的特别大的值，却又很多相对小的值，但其仍然对最优化解有significant的贡献。但从最优化问题解的平滑性来看，L1范数的最优解相对于L2范数要少，但其往往是最优解，而L2的解很多，但更多的倾向于某种局部最优解。
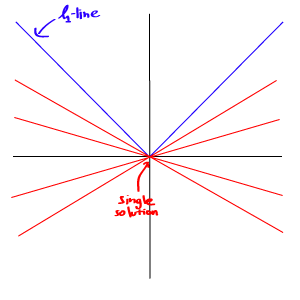
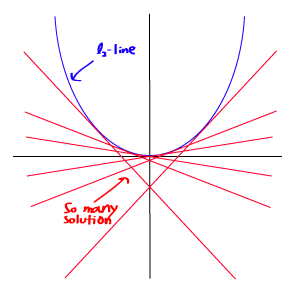
l1 norml2 norm
但由于L1范数并没有平滑的函数表示，起初L1最优化问题解决起来非常困难，但随着计算机技术的到来，利用很多凸优化算法使得L1最优化成为可能。

3- L2 范数

当然范数中最常见，也最著名的非L2范数莫属。其应用也几乎包括科学和工程的各个领域。定义公式如下：

$$ \left| \left| x \right| \right|_{2}\; :=\; \sqrt{\sum_{i=1}^{n}{x_{i}^{2}}} \tag{5} $$
也Euclidean Norm，如果用于计算两个向量之间的不同，即是Euclidean Distance.
欧几里德范数的最优化问题可以用如下公式表述： $$ \min \; \left| \left| x \right| \right|_{2}\; subject\; to\; Ax\; =\; b \tag{6} $$ 借助拉格朗日乘子，我们便可以解决该最优化问题。由L2衍生，我们还可以定义无限norm，即l-infinity norm： $$ \left| \left| x \right| \right|_{\infty }\; :=\; ^{\infty }\sqrt{\sum_{i=1}^{n}{x_{i}^{\infty }}} \tag{7} $$ 一眼看上去上面的公式还是有点tricky的。我们通过一个简单的数学变换，假设X_j是向量中最大的元素，则根据无限大的特性，我们可以得到： $$ x_{j}^{\infty }\; >>\; x_{i}^{\infty }\; \vee j\neq i $$ 则可知 $$ \sum_{i=1}^{n}{x_{i}^{\infty }\; =\; x_{j}^{\infty }} $$ 则根据公式（7）的定义，我们可以得到： $$ \left| \left| x \right| \right|_{\infty }\; =\; ^{\infty }\sqrt{\sum_{i=1}^{n}{x_{i}^{\infty }}}\; =\; ^{\infty }\sqrt{x_{j}^{\infty }}\; \; =\; \left| x_{j} \right| $$ 因此我们便可以说l-infinity norm是X向量中最大元素的长度。 $$ \left| \left| x \right| \right|_{\infty }\; =\; \max \left( \left| x_{j} \right| \right) \tag{8} $$

4- 机器学习中的应用

不知道有多少人是因为机器学习中的正则化和特征选择等才开始了解这些范数的，至少我是。L0范数本身是特征选择的最直接最理想的方案，但如前所述，其不可分，且很难优化，因此实际应用中我们使用L1来得到L0的最优凸近似。L2相对于L1具有更为平滑的特性，在模型预测中，往往比L1具有更好的预测特性。当遇到两个对预测有帮助的特征时，L1倾向于选择一个更大的特征。而L2更倾向把两者结合起来。

4-1 正则化

在机器学习中正则化是指在损失函数中通过引入一些额外的信息，来防止ill-posed问题或过拟合问题。一般这些额外的信息是用来对模型复杂度进行惩罚（Occam's razor）。其一般形式如下：
$$ Loss\left( X,Y \right)\; =\; \mbox{E}rror\left( X,Y \right)\; +\; \alpha \left| \left| w \right| \right| \tag{9} $$ \(\; \left| \left| w \right| \right|\)便可以选取L1或是L2范数来作为惩罚项，不同的模型，其损失函数也不同，对于线性回归而言，如果惩罚项选择L1，则是我们所说的Lasso回归，而L2则是Ridge回归。下面我们列出了不同模型中的正则化的损失函数（来自Andrew Ng的Machine Learning课程）：
Regularized Logistic Regression $$ J\left( \theta \right)\; =\; -\; \frac{1}{m}\left[ \sum_{i=i}^{m}{y^{\left( i \right)}\log h_{\theta }\left( x^{\left( i \right)} \right)\; +\; \left( 1-y^{\left( i \right)} \right)\log \left( 1\; -\; h_{\theta }\left( x^{\left( i \right)} \right) \right)} \right]\; +\; \frac{\lambda }{2m}\sum_{j=1}^{n}{\theta _{j}^{2}} $$ Regularized Neural Network $$ J\left( \theta \right)\; =\; -\; \frac{1}{m}\left[ \sum_{i=i}^{m}{\sum_{k=1}^{K}{y_{k}^{\left( i \right)}\log \left( h_{\theta }\left( x^{\left( i \right)} \right) \right)_{k}}\; +\; \left( 1-y^{\left( i \right)} \right)\log \left( 1\; -\; \left( h_{\theta }\left( x^{\left( i \right)} \right) \right)_{k} \right)} \right]\; +\; \frac{\lambda }{2m}\sum_{l=1}^{L-1}{\sum_{i=1}^{s_{l}}{\sum_{j=1}^{s_{l}+1}{\left( \theta _{ji}^{\left( l \right)} \right)^{2}}}} $$ Soft Margin SVM $$ \frac{1}{2}|w|^2+C\sum_i\max(0,1-y_i(w^\intercal x_i+b)) $$ 从上面可以看出常用的正则化项多是L2范数，除了防止过拟合的问题，还有一个好处就是能否改善ill-posed(condition)问题。尤其是当训练样本相对于特征数非常少时，其矩阵便是非满秩的，往往倾向于有无数个解，且是不可逆的。其condition num便会很大。一方面，根据此得到的最优化值很不稳定，往往某个特征变量很小的变动都会引发最终结果较大的偏差。另外通过矩阵求逆从而求的最优解就会变的非常困难。如对于线性回归而言，求的最优解析解为： $$ w^{ˆ}\; =\; \left( X^{T}X \right)^{-1}X^{T}y $$ 而加上L2正则项后，其变为： $$ w^{\cdot }\; =\; \left( X^{T}X\; +\; \lambda I \right)^{-1}X^{T}y $$ 从而可以直接求逆，改善了condition number。
而对于无解析解，通过迭代优化的算法，L2正则化通过将目标函数变为λ-strongly convex（λ强凸），有效的加快了其收敛速度。

4-2 贝叶斯先验

正则化项从贝叶斯学习理论的角度来看，其相当于一种先验函数。即当你训练一个模型时，仅仅依靠当前的训练集数据是不够的，为了实现更好的预测（泛化）效果，我们还应该加上先验项。而L1则相当于设置一个Laplacean先验，去选择MAP（maximum a posteriori）假设。而L2则类似于 Gaussian先验。如下图所示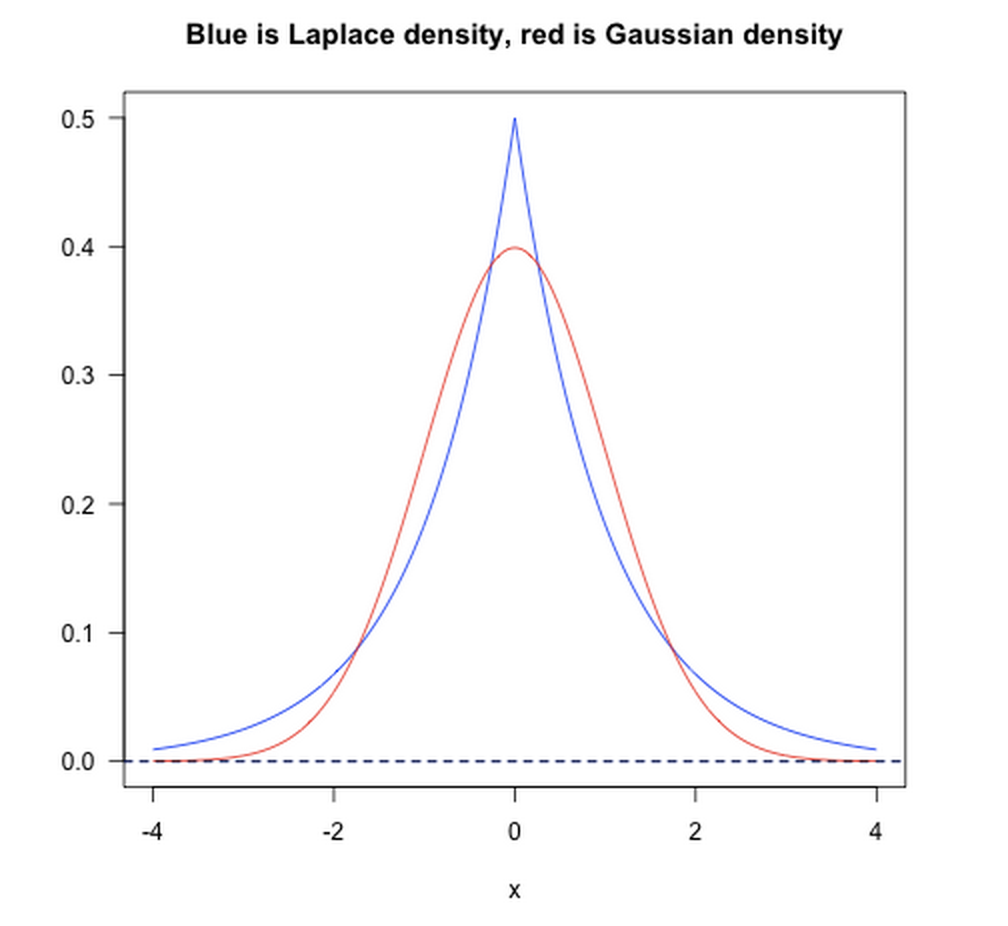：bayes l1, l2
从上图可以看出，L1先验对大值和小值的tolerate都很好，而L2先验则倾向于均匀化大值和小值。

4-3 特征选择与稀疏编码

机器学习社区里通常把特征选择的方法分为三种。一种是基于统计学的一些方法，对特征进行预筛选，选出子集作为模型输入。如统计推理使用的假设检验，P值。另一种是采用某种成熟的学习算法进行特征选择，如决策树中采用信息增益来选择特征。还有一种便是在模型算法中进行自动特征选择。而L1范数作为正则化项，其特征选择的图谱倾向于spiky，实现了有效的特征选择。
稀疏编码也是想通过寻找尽可能少的特征表达某个输入的向量X。
$$ \min \; a_{i}^{\left( j \right)},\phi _{i}\; \; \sum_{j=1}^{m}{\left| \left| x^{\left( j \right)}-\sum_{i=1}^{k}{a_{i}^{\left( j \right)}\phi _{i}} \right| \right|^{2}\; +\; \lambda \sum_{i=1}^{k}{\mbox{S}\left( a_{i}^{\left( j \right)} \right)}} $$ 其中\(\phi _{i}\)是所要寻找的基向量，\(a_{i}^{\left( j \right)}\)是我们要优化的各个基向量的权重。最右边的表达式便是其正则化惩罚项，在这里也称Sparse Cost。实际中我们通常便用L1范数。

5 参考

[1.] Wiki: Norm.
[2.] Rorasa's blog.
[3.] MaxJax.
[4.] 机器学习中的范数规范化.
[5.] Difference between l1 and l2.
[6.] gradient-descent-wolfe-s-condition-and-logistic-regression.